Skip to main content

Research group

Research group

Our group’s research concerns the theoretical and computational rheology (deformation and flow properties) of soft materials and complex fluids such as colloids, emulsions, foams, microgels, surfactants, liquid crystals and polymers, as well as their biological counterparts such as bioactive fluids and biological tissues. A particular current focus is on uncovering general principles to underpin a new understanding of how these materials yield from an initially solid-like to finally liquid-like state, and how this process can be optimally controlled in engineering applications. Another key aim is the development of constitutive models of yield stress rheology that can be used in computational fluid dynamics to predict the flows of yield stress fluids in complicated flow situations. Methods used range from direct particle simulations through mesoscale statistical mechanical descriptions to continuum constitutive models and computational fluid dynamics. A broader aim is to cross fertilise the understanding that we develop here in the context of soft materials to help understand yielding in geophysical systems such as avalanches, mudslides, lava flows, etc., and in the way that biological tissue reshapes itself under the internal stresses generated by cell division. We are also interested in flow instabilities more generally. These include the formation of shear bands in an applied shear flow, necking in extensional flows, “edge-fracture” at sheared free surfaces, and fluid-fluid demixing. We have also studied the flow of complex fluids in complicated geometrical environments such as porous media.

The work forms several distinct yet related strands:

  1. Dynamics and rheology of yield stress fluids.
  2. Shear banding in complex fluids.
  3. Extensional necking instabilities in complex fluids.
  4. Edge fracture in complex fluids.
  5. Flows in porous media.
  6. Fluid-fluid demixing.
  7. Biologically active fluids, and biological tissue dynamics.

Further details on each of these topics are below.

Current group members are:

1. Dynamics and rheology of yield stress fluids

Many soft materials defy our conventional notions of liquid versus solid, instead behaving as so called “yield stress fluids”: below a critical imposed load they show solid-like behaviour, whereas above it they yield and flow like a liquid. Examples include:

  • foams
  • dense emulsions
  • colloidal suspensions
  • surfactant onion phases
  • microgel suspensions
  • biological tissues
  • geological lava flows

Our work aims to understand this fascinating rheological behaviour via a multiscale approach that spans from direct particle based simulations through mesoscopic elastoplastic descriptions to continuum constitutive modelling and computational fluid dynamics.

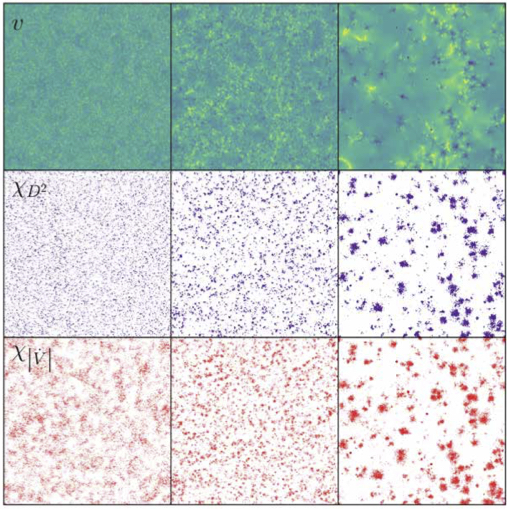
Particularly exciting recent developments have revealed novel dynamics in dense athermal suspensions of soft particles, as exemplified below in patches of “hot-spots” that coarsen over time from left to right. Shown are the particle speeds (top), thresholded local non-affine deformation rate (middle) and thresholded rate of change of particle potential energy (bottom). This work, with Rahul Chacko and Peter Sollich of Goettingen University, has just been highlighted as an “Editor’s Suggestion” in Physical Review Letters.


With Gerhard Jung of Innsbruck University, we have recently developed a simulation method capable of resolving for the first time the way the bulk rheological behaviour of an athermal suspension of soft particles (shown in blue) is governed by the boundary physics where the sample makes contact with the hard walls of its flow container (shown in black). This potentially opens a pathway to elucidating how we can ultimately seek to control bulk flows in applications such as 3D printing, by a careful tailoring of the boundary conditions.


In collaboration with our experimental partners Sebastien Manneville of ENS Lyon and Thibaut Divoux at MIT, we have also recently studied the formation of shear bands during the slow process whereby a soft material fluidises from an initially solid-like state into a finally fluid-like flowing state, thereby establishing a link with research area 2. below.

Collaborations/links

2. Shear banding in complex fluids

Complex fluids such as surfactant solutions, polymers and liquid crystals commonly show flow instabilities when subject to shear. Often these instabilities lead to the formation of macroscopic “shear bands” of differing viscosity and internal structure.

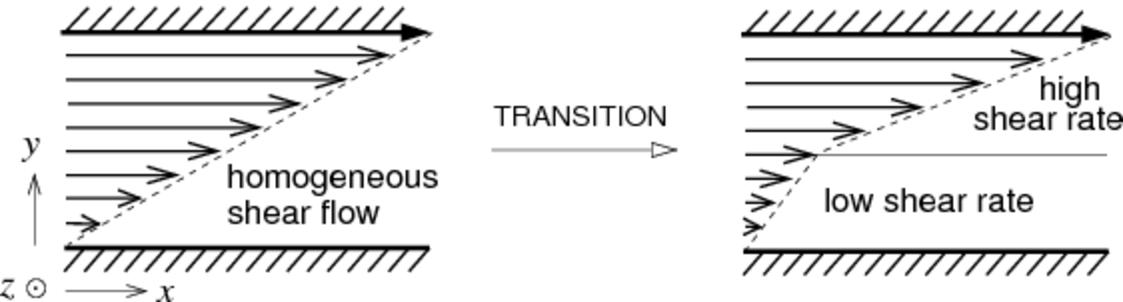
This effect can be viewed as a non-equilibrium (flow-induced) phase transition. Indeed, much of the phenomenology mirrors that of conventional (equilibrium) phase transitions, and we have pursued this analogy to study the kinetics of band formation, as well as to construct flow phase diagrams for the ultimate banded state. At the same time, there are fundamental differences from the equilibrium case, for example in the way the coexistence state is selected in the absence of a free energy minimisation principle.

Particularly exciting developments have concerned the chaotic dynamics of shear banded flows, studying both the possibility of a bulk instability of one band, as shown in this shear rate greyscale:

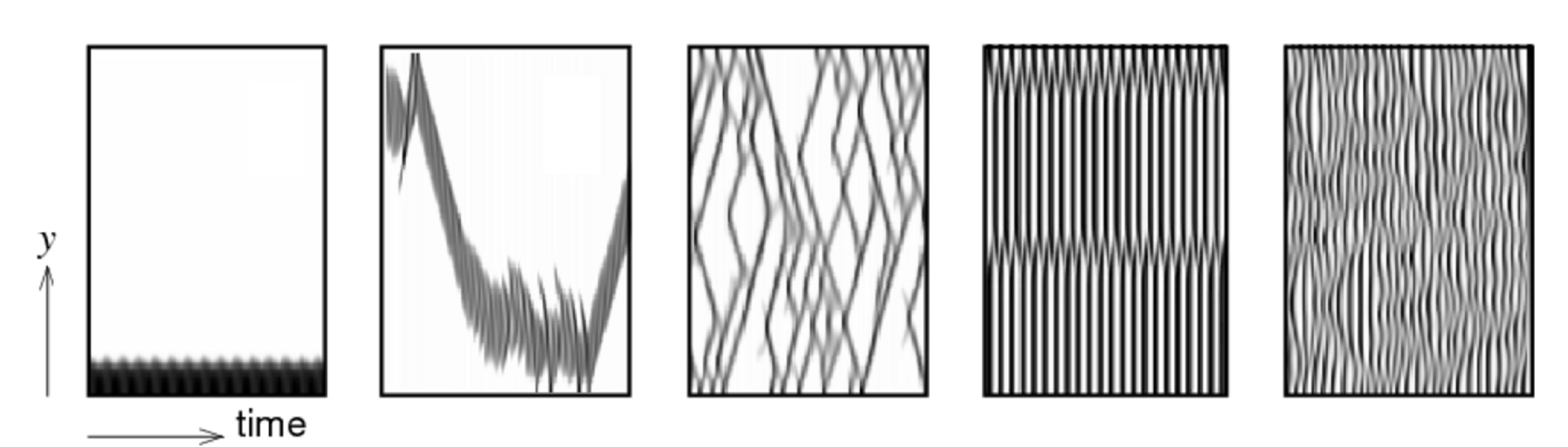
and of an instability of the interface between the bands:


The most recent focus has been on establishing that, besides those fluids that show shear banding as their ultimate long-time response to a steadily imposed shear flow, many (indeed possibly even all) complex fluids have a tendency to display banding in flows with a strong enough time-dependence, even if they are incapable of supporting it as their ultimate response to steady shear. This tendency can manifest itself transiently (for example in a shear startup protocol, during the process whereby a steady flowing state is estabilished out of an initial rest state), or in a sustained way in imposed flows (such as large amplitude oscillatory shear) that themselves have a sustained time-dependence.

Collaborations/links:

3. Extensional necking in complex fluids

Besides shear flows, complex fluids are also widely subject to extensional deformations. In an industrial context these form the basis of spinning polymeric materials into fibres for textiles, for example. In fluid dynamical terms, extensional flows cause material elements to separate exponentially quickly and so subject the underlying macromolecules to greater stretching and reorientation than shear. Indeed extensional flow response is very sensitive to underlying molecular details (linear vs. branched polymer chains, for example), and many nonlinear flow effects manifest themselves only in extension.

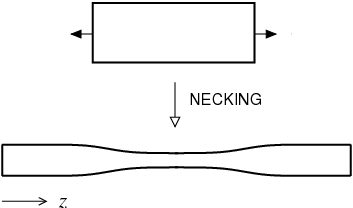
Experimentally, notable extensional devices include the filament stretching rheometer in which a cylindrical sample of fluid is sandwiched between concentric circular end-plates that are then pulled apart to draw the sample out in length. Though the aim in such devices is to achieve homogeneous extensional flow for convenient comparison with theory, more complicated features often arise. Particularly serious is the widespread occurrence of extensional necking instabilities in which any small indentations in cross-sectional area become ever more pronounced until part of the sample thins to the point of failures. Recent work has focused on deriving a general criterion for the onset of necking, applicable to a broad class of viscoelastic materials.

Collaborations/links

4. Edge fracture in complex fluids

Edge fracture is a free surface instability that widely arises when a viscoelastic material is sheared in an open flow cell. It has been cited as the most significant limiting factor in experimental shear rheometry. The aim of this work is to elucidate a full mechanistic understanding of this phenomenon in a combined theory/simulation study, and to suggest a way experimentalists might mitigate it, potentially enabling them to achieve and measure faster flows than hitherto.

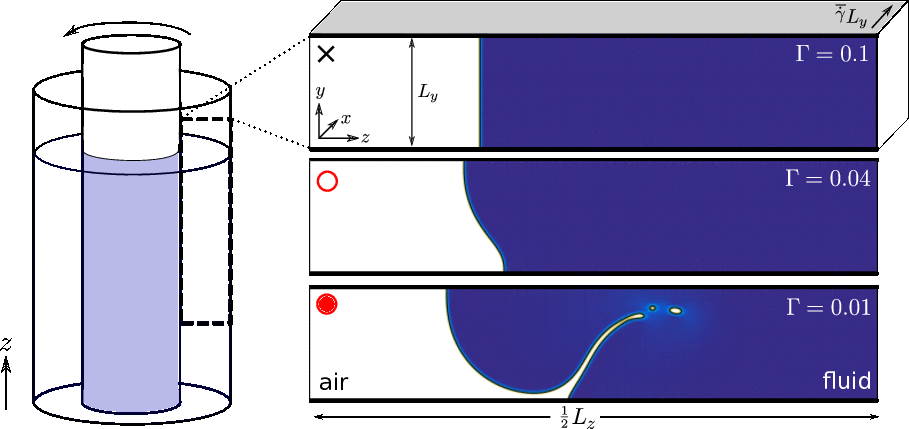
Collaborations/links

  • Prof. Roger Tanner (Emeritus, Sydney University).

5. Flows in porous media

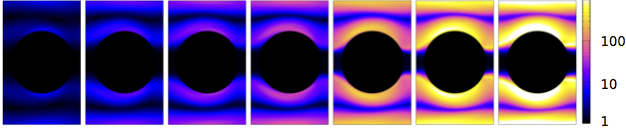
We have studied the flow of complex polymeric fluids through geometrically complicated environments such as porous media. The image below shows the degree to which the chainlike polymer molecules are deformed in flow through a single unit cell of a periodic porous medium. Snapshots from left to right correspond to increased overall throughput rate, leading to progressively stronger deformation of the polymer chains.

6. Fluid-fluid demixing

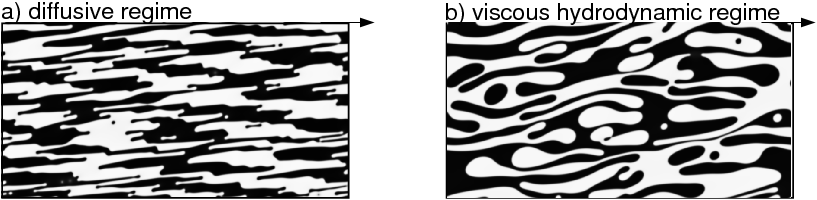
When an initially homogeneous mixture of two fluids (A and B) undergoes a deep temperature quench into the spinodal regime, it phase separates into well defined domains of A-rich and B-rich fluid. These then slowly coarsen in time through the action of the surface tension in the interfaces that separate them, such that the excess interfacial energy of the system progressively relaxes towards its minimal equilibrium value. This coarsening process proceeds through three distinct regimes that are successively dominated by diffusive, viscous and inertial dynamics. In the limit of an infinite system size, the typical domain size perpetually increases without bound: the system never globally equilibrates, even in the limit of infinite time.

Here, we consider systems that are both undergoing phase separation and simultaneously subject to an applied shear flow. The main question that we address is whether shear interrupts domain coarsening to give a nonequilibrium steady state with a typical domain size set by the inverse of the applied shear rate; or whether coarsening persists indefinitely, up to the system size, as in zero shear. For systems with inertia we have reproduced the nonequilibrium steady states reported in a recent lattice Boltzmann study by the group of Cates. The domain coarsening that would occur in zero shear is arrested by the applied shear flow, which restores a finite domain size set by the inverse shear rate. For inertialess systems, in contrast, we have found no evidence of nonequilibrium steady states free of finite size effects: coarsening persists indefinitely until the typical domain size attains the system size, as in zero shear.

7. Biologically active suspensions

In addition to fluids that are taken far from equilibrium by external driving (shearing applied at the boundaries, as in the above example), another even more challenging class of complex fluids concerns those that are driven out of equilibrium by an activity inherent within their own bulk. Examples include swarms of self-propelled bacteria or protozoa; and the viscoelastic matrix of the biological cell, in which molecular motors at cross-links between polymeric strands render the network as a whole capable of mechanical motion (in cell division or amoebic crawling). Here each mesoscopic substructure (bacterium/motor) itself individually consumes energy, and so can actively propel itself: “swimming” through the suspending fluid, or “marching” along a neighbouring cytoskeletal filament. Their collective dynamics is thus inherently far from equilibrium, even without boundary driving. Indeed in this new class of fluids the driving away from equilibrium occurs from within the volume of the fluid itself. Emergent phenomena include hydrodynamic instabilities in which an initially quiescent fluid gives way to shear banded (establishing a link to 2. above) or turbulently swirling patterns, as seen experimentally and reproduced in my simulations below.

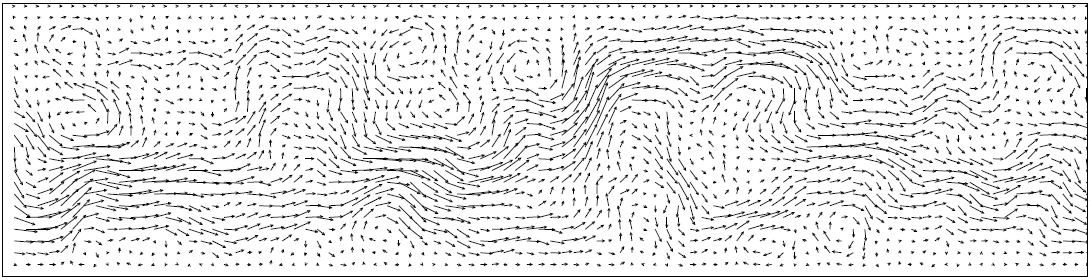
The most recent focus in this area is on developing constitutive models for the rheology of biological tissue comprising densely packed cells, considering their dynamical response to the internal stresses generated by cell division and other active processes.

Collaborations/links